| Tema | Circunferencia |
|---|---|
| Evidencia | |
| calificable? | 0 |
| Activo | 0 |
Propósito
Guía 7
Que el estudiante realice la circunferencia, identificando sus características como lugar geométrico
Motivación
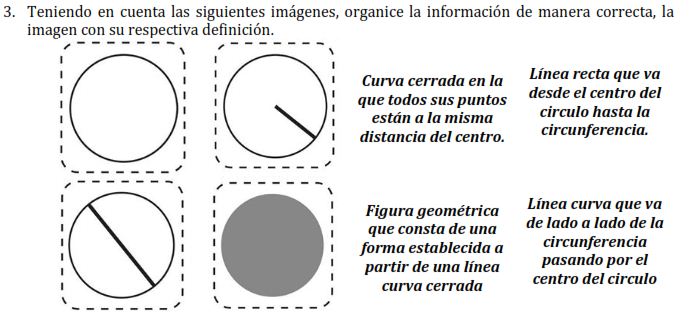
La circunferencia es una curva plana y cerrada tal que todos sus puntos están a igual distancia del centro. Distíngase de círculo, cuyo lugar geométrico queda determinado por una circunferencia y la región del plano que encierra esta.
Observar el siguiente vídeo: Concepto de Circunferencia
Explicación
La circunferencia es una línea cerrada y curva, físicamente plana, donde sus puntos están Equidistantes del punto en el centro, que se ubica en el mismo plano. En algunas ocasiones, la circunferencia suele denominarse figura geométrica cerrada donde sus puntos se encuentran a una distancia constante del centro, o que equidistan de este, es decir, a una Misma distancia del punto central; la cual se denomina radio (r). La circunferencia corresponde a un lugar geométrico de los puntos de un plano que poseen la misma distancia del punto central. Existen diversos tipos de circunferencias, los cuales son: circunferencias con un mismo centro, circunferencias tangentes a un punto fijo, circunferencias que pasan por dos puntos y Circunferencias que pasan por las intersecciones de dos circunferencias. No debemos nunca confundir el concepto de círculo con el concepto de circunferencia, que en realidad una circunferencia es la curva que encierra a un círculo (la circunferencia es una curva, el círculo una superficie).
Partes de Una circunferencia
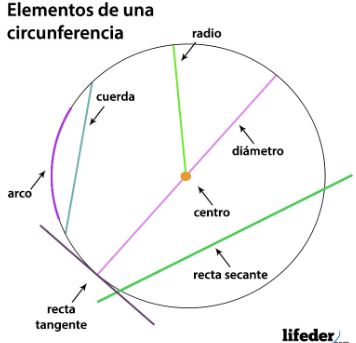
Centro (o): Se trata de un punto ubicado en el interior y centro de una circunferencia. Este se encuentra a una misma distancia de los puntos del borde de la circunferencia.
Radio (R): Es un segmento de la circunferencia que une el centro (punto central) con cualquier punto del borde. La longitud de este segmento es la mitad del diámetro, al igual que en las esferas, hiperesféras y círculos.
Diámetro: se trata de un segmento que une dos puntos opuestos de una circunferencia, pasando por el centro En otras palabras, es el segmento que al pasar por el centro, une los puntos externos de la circunferencia. La longitud del diámetro es igual a dos longitudes del radio.
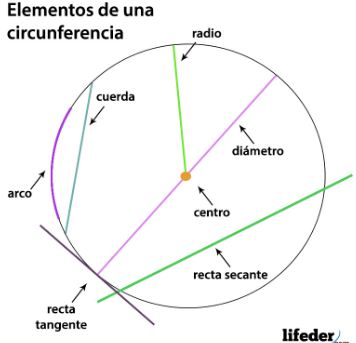
Cuerda: Se trata de un segmento que une dos puntos de una circunferencia. La cuerda de mayor longitud se conoce como diámetro.
Arco: Se trata de cada parte dividida de una cuerda de la circunferencia. Este se denota con un símbolo sobre las letras que representan los puntos extremos del mismo arco.
Recta secante: Es aquella recta que corta a la circunferencia en dos puntos cualesquiera.
Recta tangente: Es aquella recta que corta a la circunferencia en un solo punto exacto, denominado punto de tangencia. Esta recta es perpendicular al radio.
Punto de tangencia: El punto de tangencia es aquel punto de contacto entre la recta tangente y la circunferencia.
Semicircunferencia: El termino semicircunferencia representa al par de arcos delimitados por los extremos del diámetro De una circunferencia.
Ángulo central: Es un ángulo que posee su vértice en el centro y sus lados son cuerdas correspondientes a radios.
Ángulo inscrito: Este es un ángulo donde sus lados pueden ser dos cuerdas cualesquiera, y cuyo vértice se encuentra en uno de los puntos de la circunferencia.
Ejercicios


Evaluación
La evaluación es formativa e integral, por lo tanto, se tendrá en cuenta:
1. La presentación del trabajo sea impecable y muestra su dedicación.
2. Participación, realizando preguntas al profesor y retroalimentando los conocimientos.
3. Realización de todas las actividades de manera responsable y puntual.
4. La apropiación, reflexión y retroalimentación de los saberes comprendidos en el taller.
¿Cómo presentar el trabajo?
1. Se debe resolver en hoja block cuadriculadas o en el cuaderno, donde más facilite.
2. Fecha de entrega será estipulada por el profesor. Preferiblemente en PDF como se muestra en el tutorial adjunto por el profesor.
3. El trabajo se recibe el día de la fecha de entrega.
Forma de entrega:
Plataforma Sinapsis en la pestaña Tarea, o al correo: wnaranjodeo@gmail.com o al WhatsApp: 3123624081
Bibliografía
Vamos aprender Matemáticas 9°. Texto Ministerio de Educación
Foro
Cursos
| Curso | |
|---|---|
No results found. | |
Acceso a las actividades
| Actividad | Nombre | Fecha de ingreso | Fecha de actualización | Número de ingresos | Año | Curso | Subreporte |
|---|---|---|---|---|---|---|---|
No results found. | |||||||
