| Tema | Números Enteros (Z) |
|---|---|
| Evidencia | (not set) |
| calificable? | 0 |
| Activo | 0 |
Propósito
Guia 2
Que el estudiante realice operaciones de Orden y Adición de números Enteros.
Motivación
Explicación
Sebastián registro en una tabla la temperatura de tres cuartos fríos de un laboratorio.
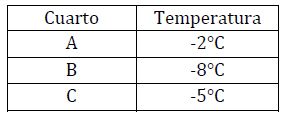
Para determinar en cual de los tres hace más frío, se pueden representar las temperaturas en una recta numérica y luego comparar su ubicación.
Cuando se comparan dos números en la recta numérica, se deduce que es mayor el número que se encuentra ubicado a la derecha del otro. A su vez, es menor el que se encuentra ubicado a la izquierda. De acuerdo con lo anterior, se puede establecer las siguientes relaciones de orden.
- Como -2 está a la derecha de -5, entonces -5 < -2.
- Como -5 está a la derecha de -8, entonces -8 < -5.
- Como -2 está a la derecha de -8, entonces -8 < -2. Esto quiere decir que el orden de las temperaturas es:
Por lo tanto el cuarto B es en el que hace más frío.
Otros criterios que permiten determinar la relación de orden existente entre dos números enteros son:
- Dados dos números enteros positivos, es mayor el que tiene mayor valor absoluto.
- Dados dos números enteros negativos, es mayor el que tiene menor valor absoluto.
- Un número positivo siempre es mayor que cualquier número negativo.
Adición de números enteros del mismo signo.
En una exploración del fondo marino, un buzo se sumerge en un primer momento 45 m de profundidad, y al cabo de una hora desciende otros 27 m. en total, ¿Cuántos metros descendió el buzo durante la
exploración?
Para resolver la situación se pueden sumar las distancias recorridas por el buzo en su descenso, es decir, se efectúa la adición de números enteros.

Analíticamente, el resultado anterior equivale a la suma de los valores absolutos de los sumandos, precedida por el signo común de los dos números.
Se deduce entonces que el buzo descendió 72 metros en total.
Adición de números enteros del diferente signo.
En la adición de números enteros de diferente signo, se restan los valores absolutos de los sumandos y a la suma se le antepone el signo del sumando que tenga el mayor valor absoluto.
PRÁCTICA Y EJECUCIÓN
Ejemplo 1
Observa los números enteros representados en la recta numérica de la imagen.
- 8 < - 4, ya que -4 está a la derecha de -8.
- 6 es el mayor de los números representados, puesto que está ubicado a la derecha de todos los demás.
- El orden de los números señalados de menor a mayor es: -9 < -8 < -4 < 3 < 6
Ejemplo 2
Para efectuar la operación -9 + 12 se procede así:
1. Se calcula los valores absolutos de los dos sumandos. |-9| = 9 y |12 | = 12
2. Al mayor valor absoluto se le resta el menor valor. 12 – 9 = 3
3. Al resultado se le antepone el signo del sumando que tenga el mayor valor absoluto. -9 + 12 = 3
Ejercicios
1. Representa cada pareja de números enteros en una recta numérica. Luego, escribe < o > según sea el caso.
a. -3 y 1
b. 4 y -6
c. -5 y -8
d. 6 y -3
e. 4 y 10
2. Ordena de menor a mayor los números de cada grupo.
a. 25, -32, 24, -1, 0, -12.
b. 12, 7, -20, 16, -13, 8.
c. -54, 678, -249, 14, 0, 190. d. 32, 56, 17, -34, -56, 2
e. 36, -65, -39, -41, 58, 72.
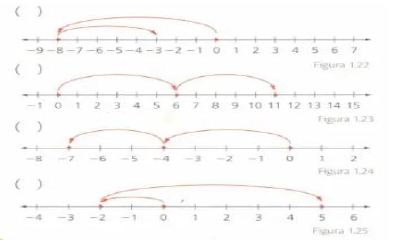
3. Relaciona cada adición con la representación en la recta numérica que le corresponde.
a. -4 + (-3) b. 6 +5 c. -2 + 7 d. -8 + 5
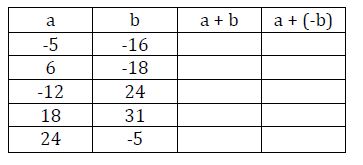
4. Calcula la suma en cada caso.
a. 19 + (-12)
b. -82 + 9
c. -6 + (-27)
d. 18 + (-2)
e. 42 + 37
Evaluación
En el espacio de tarea subir los ejercicios resueltos paso a paso y bien presentados.
Bibliografía
Vamos aprender Matemáticas 7°. Texto Ministerio de Educación
Foro
Cursos
| Curso | |
|---|---|
No results found. | |
Acceso a las actividades
| Actividad | Nombre | Fecha de ingreso | Fecha de actualización | Número de ingresos | Año | Curso | Subreporte |
|---|---|---|---|---|---|---|---|
No results found. | |||||||
