| Tema | Números reales. |
|---|---|
| Evidencia | (not set) |
| calificable? | 0 |
| Activo | 0 |
Propósito
Guía 1. Realización de operaciones con números enteros.
Motivación
Mira y escucha con detenimiento el siguiente video:
Explicación
Los números naturales: Para contar los elementos de un conjunto se utiliza el conjunto de los NUMEROS NATURALES (N). el conjunto de los números naturales se representa por extensión así:
N = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11,…}
El conjunto de los naturales se representa en la semirrecta:
Para comparar dos números naturales se utilizan los signos mayor que (>) y menor que (<).
Siempre que se suman o multiplican un par de números naturales se obtiene como resultado un número natural; sim embargo cuando se realizan una sustracción o una división, puede suceder que el resultado no pertenezca a los números naturales.
Los números enteros: En la vida real algunas cantidades toman valores positivos y negativos, por lo tanto, se debe recurrir a los números enteros. Este conjunto se representa así:
Z = {…, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6,…}
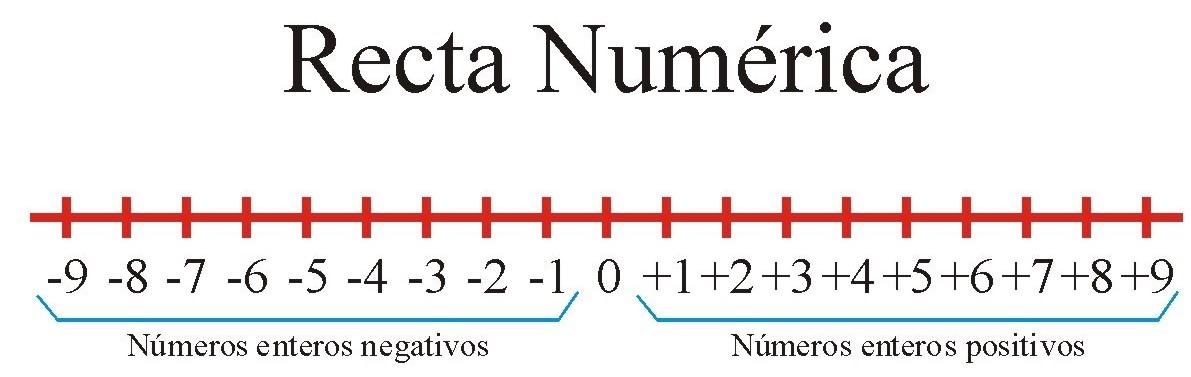
Valor absoluto: el valor absoluto de un número entero es el número natural que resulta al prescindir de su signo. Geométricamente el valor absoluto de un entero a es la distancia entre a y 0 y se denota por |a|. por ejemplo |8| = 8 y |- 6|= 6
Ejercicios
- 1. Representar cada uno de los conjuntos en una recta numérica:
- A = { n/n E N, n < 6}
- B = { n/n E N, 2 < n < 9}
- C = { n/n E N, n > 5}
- D = { n/n E N, n > 12}
- 2.colocar el paréntesis de manera que las igualdades sean ciertas:
- a. 25 – 17 – 16 = 24
- b. 29 – 25 – 20 = 24
- c. 40 – 9 – 2 = 33
- d. 21 – 12 – 7 = 16


- 5. Escribir, >, < o =; según corresponda:
- a. |- 20 | _____ | 20 |
- b.– 800 _____ - 200
- c. - | - 8 |____ 8
- d. - | 5 | ____5
- e.– 50 ÷ 5 ____ 20 x (- 2)
- f. – 150 ÷4 ____ - 35 ÷ 7.
- 6. Escribir V, si la afirmación es verdadera o F si es falsa. Luego, justificar la respuesta:
- a. Entre dos números enteros, siempre hay otro número entero.
- b. El mayor número entero negativo es el 1.
- c. El siguiente de cualquier número entero es un número mayor que él.
- d. El producto de dos enteros negativos es otro entro negativo.
- 7. Responda:
- a. Si n es un número natural par. ¿Cómo son? n + 1;n + 2;n + 3. Justificar la respuesta:
- 8. Completar los espacios en blanco con los números correspondientes:
- 4x5 + 35x2 - 8÷4 + 15 ÷3
- = ____ + ____ - ____+ ____
- = _____
Evaluación
Cada estudiante debe enviar por este medio o por WhatsApp el desarrollo de los ejercicios. Para la respectiva valoración se tiene en cuenta la puntualidad, la presentación de las actividades, la solución acertada de los ejercicios y la conectividad a las clases.
Bibliografía
Foro
Cursos
| Curso | |
|---|---|
No results found. | |
Acceso a las actividades
| Actividad | Nombre | Fecha de ingreso | Fecha de actualización | Número de ingresos | Año | Curso | Subreporte |
|---|---|---|---|---|---|---|---|
No results found. | |||||||
