| Tema | Guía No. 16: Mapas de Karnaugh. |
|---|---|
| Evidencia | |
| calificable? | 1 |
| Activo | 0 |
Propósito
Guía No. 16: Mapas de Karnaugh.
Implementar un sistema electrónico completo mediante el diseño y elaboración de Placas de Circuito Impreso.
Motivación
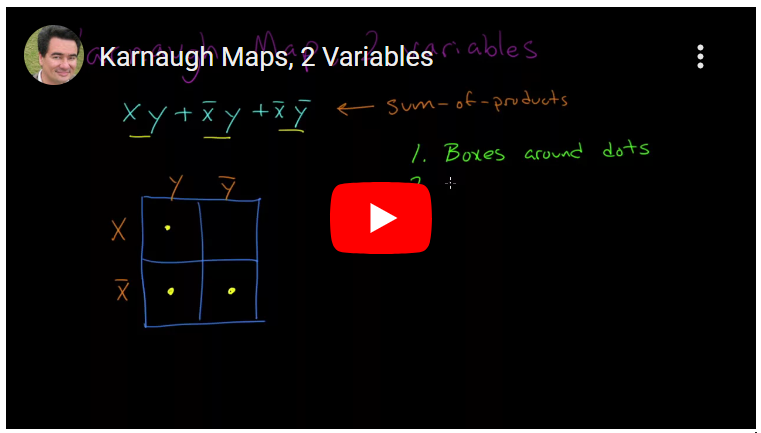
“Aquí está la expresión que vamos a simplificar, usando un mapa de Karnaugh. X e Y, no X e Y, no X no Y. Las expresiones que usamos para los mapas de Karnaugh deben estar en lo que se llama forma de suma de productos, si no es en forma de suma de productos, es posible que deba usar algunas de las propiedades del álgebra booleana, como la ley distributiva, para transformarla en esta forma. Ya que esta es una expresión de dos variables, vamos a hacer una cuadrícula de 2 X 2 con una de las variables abajo lado y la otra variable en la parte superior a continuación. Vamos a colocar un punto en cada una de las celdas que tiene un término correspondiente en la expresión aquí está el término XY, así que colocaremos un punto en la intersección de X e Y, esto no es XY, que es la celda de aquí abajo en la parte inferior izquierda y no X, no Y es la que está en esquina inferior derecha. Ahora, antes de seguir adelante, permítanme establecer cuáles son las reglas para usar un mapa de Karnaugh. La regla Número uno es colocar cuadros alrededor de todos los puntos y solo los puntos. Segundo: las dimensiones del cuadro deben ser potencias de dos, como uno por uno, dos por dos, dos por cuatro y así sucesivamente. Tercero: los cuadros deben ser lo mas grandes posible y usted debería usar la menor cantidad posible y, finalmente, la superposición está bien, así que procedamos. Queremos rodear estos tres puntos con cuadros. Vamos a ignorar esta celda, en la esquina superior derecha. Queremos usar la menor cantidad de cuadros posible y deberían ser tan grande como sea posible, así que veo dos cuadros aquí, veo uno alrededor de la columna de la izquierda y el siguiente alrededor de la fila inferior, así que solo he usado solo dos cuadros para rodear los tres puntos, son lo mas grandes posible a través de cada una de las potencias de dos y dimensión, y está bien que haya superpuesto uno de ellos. Este cuadro aquí es el cuadro Y y este cuadro no es el cuadro X y entonces la solución a esto es solo la unión de estos dos cuadros, y mas no X es la respuesta. Así es como se hace un mapa de Karnaugh para dos variables…”
Explicación
¿Qué es un mapa de Karnaugh? El mapa de Karnaugh o mapa-k es un diagrama utilizado para la simplificación de funciones algebraicas Booleanas, permitiendo de manera gráfica reconocer patrones y así reduce la necesidad de hacer cálculos extensos para la simplificación de expresiones booleanas. Ventajas del mapa de Karnaugh: El mapa-k nos permite convertir la tabla de verdad de una ecuación booleana en una forma SOP(Suma de productos) o POS(Productos de suma) minimizada; Reglas básicas y sencillas para la simplificación; La facilidad del método permite que sea más rápido y más eficiente que otras técnicas de simplificación en el Álgebra de Boole. Reglas del mapa de Karnaugh: 1.Las agrupaciones o el término a considerar únicamente serán del número “1”; 2.Las agrupaciones únicamente se deben hacer en horizontal y vertical; 3.Las agrupaciones por considerar deben contener 2n elementos. Es decir cada agrupación que contiene cada grupo tendrá 1, 2, 4, 8,…, 2n cantidad de número de uno o unos; 4.Para una mejor simplificación se debe considerar el grupo más grande posible; 5.Se debe considerar todo número “1”; 6.Es posible solapar grupos de “1”; 7.La formación de grupos también se puede producir con las celdas extremas de la tabla; 8.Debemos considerar el menor número de agrupaciones o grupos posibles obedeciendo las reglas anteriores.
Ejercicios
1. Comprar la guía y pegarla en el cuaderno.
2. Diseñar la tarjeta de circuito impreso para la etapa de alimentación.
3. Tomar una foto personalizada del producto y pegarla en el cuaderno.


Evaluación
1. Revisión del cuaderno; 2. Verificación del funcionamiento del sistema implementado.
3. Permanencia en el puesto de trabajo; 4. Uso adecuado de materiales
5. Habilidad en el manejo de herramientas.
Bibliografía
Foro
Acceso a las actividades
| Actividad | Nombre | Fecha de ingreso | Fecha de actualización | Número de ingresos | Año | Curso | Subreporte |
|---|---|---|---|---|---|---|---|
No results found. | |||||||
